DEDUCCIÓN DE LA FÓRMULA:
La ecuación de forma general se escribe así:
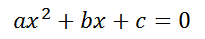
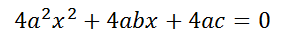

El siguiente paso es mover el término 4ac al lado derecho de la ecuación
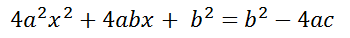
Si nos fijamos en el lado izquierdo, vemos que hay desarrollado un producto notable, si sacamos la raíz cuadrada del primer y tercer término y vemos que el segundo término es el doble del producto de esas raíces:
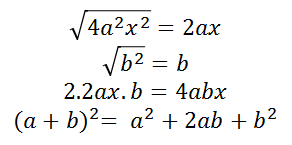
La última igualdad puede escribirse así:
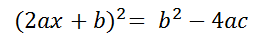
Sacamos la raíz cuadrada en ambos lados y ponemos un +- a la izquierda (según los criterios de equivalencia):
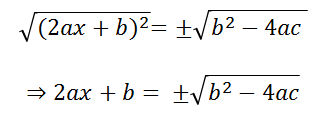
Al acabar y despejar la x como resultado queda la fórmula:
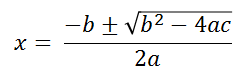
En el resultado final tenemos la fórmula escrita de manera condensada (representado por el símbolo ± delante de la raíz, pero también podemos escribirla, separando las soluciones o raíces de la siguiente forma:
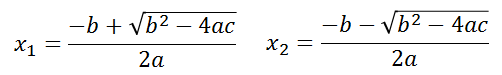
DISCRIMINANTE
La cantidad que está dentro de la raíz es el discriminante que se representa con este símbolo Δ.
El discriminante puede tener 3 variantes:
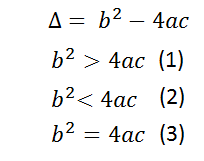
1: si la variante es la 1, se tendrán 2 soluciones
2: si la variante es la 2, el discriminante dará negativo, por lo que la ecuación no tiene soluciones.
3: si la variante es la 3, solo se tendrá 1 solución



No hay comentarios:
Publicar un comentario